문제
다음 글과 <자기소개>를 근거로 판단할 때, 대학생, 성별, 학과, 가면을 모두 옳게 짝지은 것은?
| 대학생 5명(A~E)이 모여 주말에 가면파티를 하기로 했다. ○ 남학생이 3명이고 여학생이 2명이다. ○ 5명은 각각 행정학과, 경제학과, 식품영양학과, 정치외교학과, 전자공학과 재학생이다. ○ 5명은 각각 늑대인간, 유령, 처녀귀신, 좀비, 드라큘라 가면을 쓸 것이다. ○ 본인의 성별, 학과, 가면에 대해 한 명은 모두 거짓만을 말하고 있고 나머지는 모두 진실만을 말하고 있다. |
<자기소개>
| A: 식품영양학과와 경제학과에 다니지 않는 남학생인데 드라큘라 가면을 안 쓸 거야. B: 행정학과에 다니는 남학생인데 늑대인간 가면을 쓸 거야. C: 식품영양학과에 다니는 남학생인데 처녀귀신 가면을 쓸 거야. D: 정치외교학과에 다니는 여학생인데 좀비 가면을 쓸 거야. E: 전자공학과에 다니는 남학생인데 드라큘라 가면을 쓸 거야. |
대학생 성별 학과 가면
① A 여 행정학과 늑대인간
② B 여 경제학과 유령
③ C 남 식품영양학과 좀비
④ D 여 정치외교학과 드라큘라
⑤ E 남 전자공학과 처녀귀신
한 명은 모두 거짓만을 말하고 있고 나머지는 모두 진실만을 말하고 있으므로 한 명씩 진실(T)과 거짓(F)인 경우를 대입해본다. 이는 언어논리에서 진리값을 확정하기 위한 ‘귀류법’을 활용하는 방식과 동일하다.
(1) A가 거짓(F)인 경우
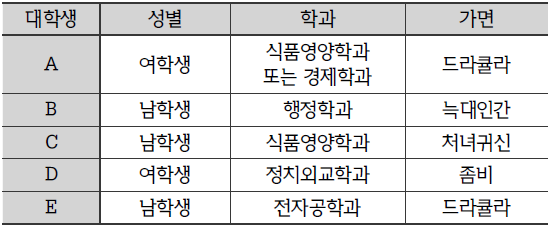
A가 거짓(F)인 경우 성별은 조건을 충족한다.
학과도 A가 경제학과가 가능하므로 조건을 충족한다.
그러나 가면에서 A의 드라큘라가 E와 중복되어 모순이 발생한다.
따라서 A는 반드시 진실(T)이 된다.
이를 통해 ①번 선지를 소거한다.
(2) B가 거짓(F)인 경우

B가 거짓(F)인 경우 성별은 조건을 충족한다.
학과는 C, D, E가 고정되어 있는 상황에서 B가 행정학과가 아니므로 경제학과로 확정된다. A는 행정학과로 확정된다. 가면에서 C, D, E가 고정되어 있는 상황에서 B가 늑대인간이 아니므로 유령으로 확정된다. 이로 인해 A는 늑대인간으로 확정된다. 따라서 B가 거짓(F)인 경우에는 모순이 발생하지 않고 모든 항목이 확정된다.
※ 다른풀이: 선지를 소거하는 방법으로 문제를 해결할 수 있다.
(1) 성별조건: 남학생 3명, 여학생 2명
참은 4명이고 거짓은 1명이다. 현재의 상황에서 D를 거짓(F)으로 가정한다면 남학생이 5명이 되어 여학생이 아무도 없게 된다. 따라서 D는 반드시 진실(T)임을 확인할 수 있다.
D는 <자기소개>에서 좀비가면을 쓴다고 진술하였으나 ④번 선지에서는 드라큘라 가면을 제시하였으므로 ④번은 틀린 선지가 된다.
④번 선지를 소거한다.
(2) 학과조건: 행정학과, 경제학과, 식품영양학과, 정치외교학과, 전자공학과
<자기소개>의 학과에 대한 진술을 보면 B, C, D, E는 특정 학과를 다닌다고 언급하고 있지만 A는 특정학과를 다니지 않는다고 언급하고 있다. 이를 통해 A의 진술이 특이하다는 점을 확인할 수 있다.
현재의 상황에서 A를 거짓(F)으로 가정한다면 A는 식품영양학과 또는 경제학과로 확정할 수 있다. 나머지가 진실(T)이므로 A를 경제학과로 확정할 수 있어 학과 조건에는 모순이 발생하지 않는다. 그러나 ①번 선지에서 A는 행정학과라고 언급하고 있어 모순이 발생하게 된다. 따라서 A는 반드시 진실(T)임을 확인할 수 있다.
①번 선지를 소거한다.
(3) 가면조건: 늑대인간, 유령, 처녀귀신, 좀비, 드라큘라
성별조건과 학과조건을 통해 A와 D가 반드시 진실(T)임을 확인하였다면 현재의 상황은 다음과 같다.

현재의 상황에서 E를 거짓(F)으로 가정한다면 E는 드라큘라 가면을 쓰지 않는다. 그러나 이 경우 아무도 드라큘라 가면을 쓰지 않게 되어 모순이 발생한다. 따라서 E는 반드시 진실(T)임을 확인할 수 있다. ⑤번 선지를 소거한다.
진릿값이 확정되지 않은 B와 C에 거짓(F)을 하나씩 대입하여 성별, 학과, 가면 충족여부를 다시 검토한다.
B를 거짓(F)으로, C를 진실(T)로 가정한다면 B는 여학생이 되어 성별조건을 충족한다. 또한 행정학과가 아니므로 남아있는 학과인 경제학과로 확정할 수 있다. 또한 늑대인간 가면을 쓰지 않으므로 남아있는 가면인 유령으로 확정할 수 있다. 이로 인해 A는 행정학과, 늑대인간 가면으로 확정된다. 따라서 모순이 발생하지 않는다.
'5급 공채 (행정고시) > 2019년 가책형' 카테고리의 다른 글
| [19행(가)-3940해] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 39-40번 해설 (0) | 2021.10.24 |
|---|---|
| [19행(가)-3940] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 39-40번 (0) | 2021.10.24 |
| [19행(가)-36해] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 36번 해설 (0) | 2021.10.24 |
| [19행(가)-36] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 36번 (0) | 2021.10.24 |
| [19행(가)-33] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 33번 (0) | 2021.10.21 |
| [19행(가)-30해] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 30번 해설 (0) | 2021.10.21 |
| [19행(가)-30] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 30번 (0) | 2021.10.21 |
| [19행(가)-27해] 2019년 5급 공채 (행정고시) PSAT 상황판단 가책형 27번 해설 (0) | 2021.10.21 |






댓글