문제
다음 글을 근거로 판단할 때, <보기>에서 옳은 것만을 모두 고르면?
키가 서로 다른 6명의 어린이를 다음 그림과 같이 한 방향을 바라보도록 일렬로 세우려고 한다. 그림은 일렬로 세운 하나의 예이다. 한 어린이(이하 甲이라 한다)의 등 뒤에 甲보다 키가 큰 어린이가 1명이라도 있으면 A방향에서 甲의 뒤통수는 보이지 않고, 1명도 없으면 A방향에서 甲의 뒤통수는 보인다. 반대로 甲의 앞에 甲보다 키가 큰 어린이가 1명이라도 있으면 B방향에서 甲의 얼굴은 보이지 않고, 1명도 없으면 B방향에서 甲의 얼굴은 보인다.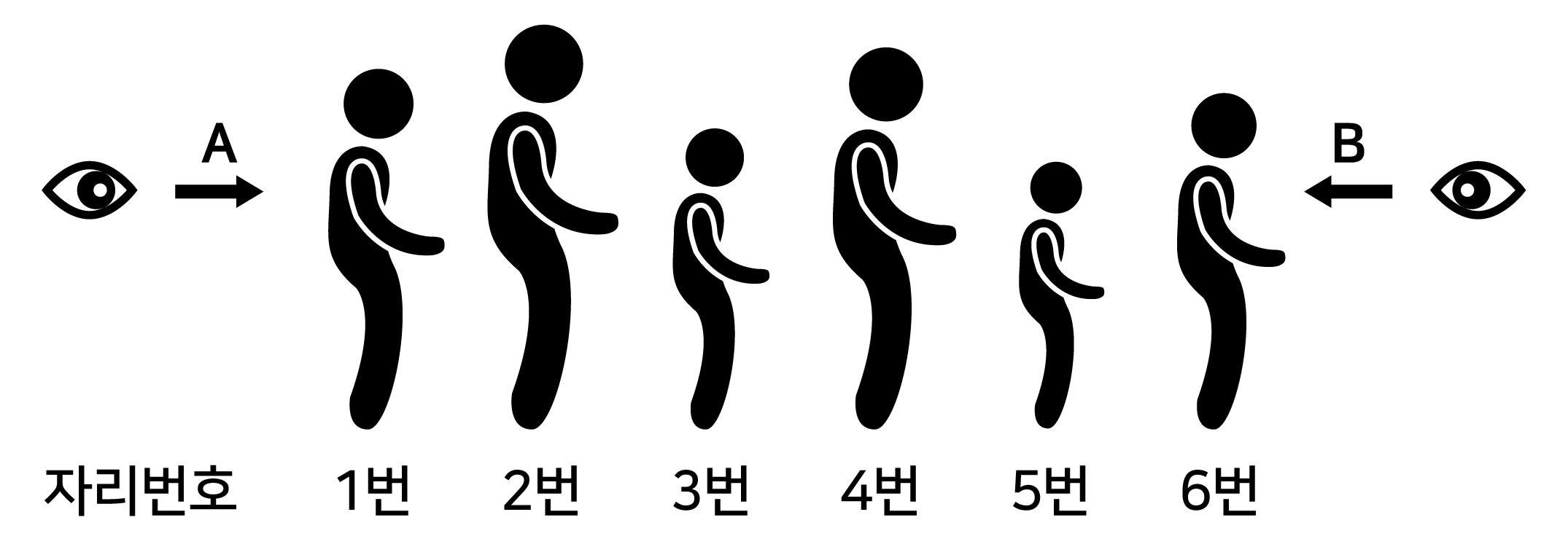 |
<보 기>
| ㄱ. A방향에서 보았을 때 모든 어린이의 뒤통수가 다 보이게 세우는 방법은 1가지뿐이다. ㄴ. 키가 세 번째로 큰 어린이를 5번 자리에 세운다면, A방향에서 보았을 때 그 어린이의 뒤통수는 보이지 않는다. ㄷ. B방향에서 2명의 얼굴만 보이도록 어린이들을 세웠을 때, A방향에서 6번 자리에 서 있는 어린이의 뒤통수는 보이지 않는다. ㄹ. B방향에서 3명의 얼굴이 보인다면, A방향에서 4명의 뒤통수가 보일 수 없다. |
① ㄱ, ㄴ
② ㄷ, ㄹ
③ ㄱ, ㄴ, ㄷ
④ ㄱ, ㄷ, ㄹ
⑤ ㄴ, ㄷ, ㄹ
ㄱ. (O) (반례) A방향에서 보았을 때 모든 어린이의 뒤통수가 다 보이게 세우는 방법이 2가지 이상인 반례를 찾는다. A방향에서 보는 경우 모든 어린이의 뒤통수가 다 보이는 경우는 우선 키가 작은 순서로 1번부터 6번까지 배치하는 것이다. 모든 어린이는 세운 후 모든 어린이의 뒤통수가 현재 상황에서 키가 가장 작은 어린이가 있는 1번의 바로 앞에 서있지 않은 다른 4명의 어린이가 오게 된다면 최소한 1명의 어린이의 뒤통수가 보이지 않게 된다. 이에 따라 방향에서 보았을 때 모든 어린이의 뒤통수가 다 보이게 세우는 방법은 1가지뿐이다. 반례가 없으므로 ㄱ은 옳은 선지가 된다.
ㄴ. (O) (반례) 키가 세 번째로 큰 어린이를 5번 자리에 세운다면, A방향에서 보았을 때 그 어린이의 뒤통수가 보이는 반례를 찾는다. 우선 키가 세 번째로 큰 어린이를 5번 자리에 세운다. 세 번째로 큰 어린이의 뒤통수가 보이기 위해서는 키가 두 번째로 큰 어린이와 키가 가장 큰 어린이를 6번 이후로 세워야 한다. 그러나 6번은 한자리만 있으므로 키가 두 번째로 큰 어린이와 키가 가장 큰 어린이 중 적어도 한 명은 5번 이전으로 세워지게 된다. 이에 따라 A방향에서 보았을 때 그 어린이의 뒤통수는 보이지 않게 된다. 반례가 없으므로 ㄴ은 옳은 선지가 된다.
ㄷ. (O) (반례) B방향에서 2명의 얼굴만 보이도록 어린이들을 세웠을 때, A방향에서 6번 자리에 서 있는 어린이의 뒤통수가 보이는 반례를 찾는다. B방향에서 2명의 얼굴만 보이는 경우는 키가 가장 큰 어린이의 위치를 6번을 제외하고 1번~5번 중 어느 곳에 세워도 가능하다. 다음으로 키가 두 번째로 큰 어린이를 6번에 고정시키면 B방향에서 2명의 얼굴만 보이게 된다. 그러므로 A방향에서 보면 6번에 고정된 키가 두 번째로 큰 어린이의 뒤통수는 항상 키가 가장 큰 어린이에게 가려 보이지 않게 된다. 반례가 없으므로 ㄷ은 옳은 선지가 된다.
ㄹ. (X) (반례) B방향에서 3명의 얼굴이 보일 때 A방향에서 4명의 뒤통수가 보이는 반례를 찾는다. 우선 A방향 기준으로 키가 작은 순서부터 1번부터 3번까지 세운다. 다음으로 4번부터 6번까지 키가 큰 순서부터 세우면 B방향에서 3명의 얼굴이 보이면서(4, 5, 6번 자리의 얼굴이 보임) A방향에서 4명의 뒤통수가 보이는(1, 2, 3, 4번의 뒤통수가 보임) 반례가 있음을 확인할 수 있다. 따라서 반례가 있으므로 ㄹ은 틀린 선지가 된다.
'5급·7급 민간경력자 > 2020년 가책형' 카테고리의 다른 글
| [20민(가)-23해] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 23번 해설 (735) | 2021.08.10 |
|---|---|
| [20민(가)-23] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 23번 (322) | 2021.08.10 |
| [20민(가)-22해] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 22번 해설 (0) | 2021.08.10 |
| [20민(가)-22] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 22번 (0) | 2021.08.10 |
| [20민(가)-21] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 21번 (0) | 2021.08.10 |
| [20민(가)-20해] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 20번 해설 (0) | 2021.08.10 |
| [20민(가)-20] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 20번 (0) | 2021.08.10 |
| [20민(가)-19해] 2020년 5급/7급 민간경력자(민경채) PSAT 상황판단 가책형 19번 해설 (0) | 2021.08.10 |






댓글